亲爱的数学迷们，今天我们要来聊聊一个既神秘又有趣的数学概念——反函数公式。想象你手中有一张神奇的地图，它能够将你从A点带到B点，然后再从B点带你回到A点。这听起来是不是很神奇？没错，这就是反函数公式能为你做到的！

什么是反函数公式？

反函数公式，简单来说，就是将一个函数的输入和输出互换后，依然保持原函数性质的一种数学工具。它就像一把钥匙，能解锁函数世界的秘密。举个例子，假设你有一个函数f(x) = 2x 3，那么它的反函数f^(-1)(y)就是将x和y互换后，解出y关于x的表达式。这样，你就可以用这个反函数来找到任何y值对应的x值了。

反函数公式的求法

想要找到反函数，其实并没有那么难。下面，我就来为你揭秘反函数公式的求法。

1. 确定原函数的定义域和值域：这是求反函数的第一步，因为反函数的定义域就是原函数的值域。

2. 判断原函数是否为一一对应的：只有当函数是一一对应的，即每个y值都对应唯一的x值时，它才有反函数。

3. 交换x和y的位置：将原函数的方程中的x和y互换位置，得到一个新的方程。

4. 解出y关于x的表达式：通过解这个新方程，你就能得到反函数的表达式。

5. 将得到的表达式中的y替换为f(x)：这样，你就得到了原函数的反函数。

反函数公式的应用

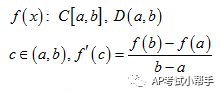
反函数公式不仅在数学理论研究中非常重要，而且在实际应用中也有着不可忽视的作用。下面，我就来为你列举几个反函数公式的应用场景。

1. 解方程：反函数公式可以帮助我们解一些看似复杂的方程。比如，对于方程y = 2x 3，我们可以通过求其反函数来解出x的值。

2. 求不等式的解集：反函数公式还可以用来求不等式的解集。比如，对于不等式2x 3 > 7，我们可以通过求其反函数来找到满足不等式的x值范围。

3. 工程和物理学中的转换问题：在工程和物理学中，反函数公式可以用来解决各种转换问题。比如，在电路设计中，反函数公式可以帮助我们找到电路元件的参数。

反函数公式的证明

你可能好奇，反函数公式是如何被证明的呢？其实，证明反函数公式的方法并不复杂。首先，我们需要确认原函数具有反函数存在的条件，即原函数必须是一一对应的。通过解原函数的方程，求出x关于y的表达式，从而得到反函数公式。

举个例子，假设我们有函数f(x) = 2x 3，我们想要找到它的反函数。我们首先设置y = 2x 3，然后解这个方程得到x = (y - 3) / 2。因此，反函数f^(-1)(y) = (y - 3) / 2。

反函数公式，这个神奇的数学工具，不仅可以帮助我们更好地理解函数的性质，还能在解决实际问题中发挥重要作用。所以，亲爱的数学迷们，让我们一起探索这个充满魅力的数学世界吧！

未经允许不得转载：黑料吃瓜网 » 反函数公式,反函数公式解析与应用概览